3. Lists and Turtle Drawing¶
Quick Overview of Day
Use lists while moving turtles.
CS20-CP1 Apply various problem-solving strategies to solve programming problems throughout Computer Science 20.
CS20-FP1 Utilize different data types, including integer, floating point, Boolean and string, to solve programming problems.
CS20-FP2 Investigate how control structures affect program flow.
CS20-FP3 Construct and utilize functions to create reusable pieces of code.
CS20-FP4 Investigate one-dimensional arrays and their applications.
3.1. Check Your Understanding¶
- Option 1
- Nice!
- Option 2
- Try again.
- Option 3
- Try again.
- Error, will not run.
- Try again.
lists-and-turtles1: What will be the result of the following code being executed?
import turtle
def draw_thing(some_turtle, tasks):
for value in tasks:
some_turtle.forward(value)
some_turtle.stamp()
some_turtle.backward(value)
some_turtle.right(30)
window = turtle.Screen()
bob = turtle.Turtle()
my_list = [10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120]
draw_thing(bob, my_list)
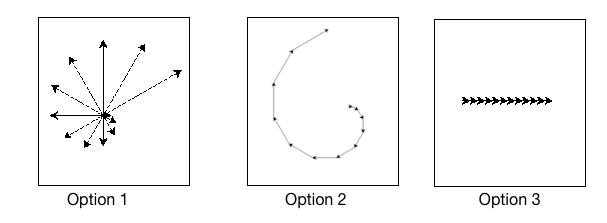
- Option 1
- Try again.
- Option 2
- Nice!
- Option 3
- Try again.
- Error, will not run.
- Try again.
lists-and-turtles2: What will be the result of the following code being executed?
import turtle
def draw_thing(some_turtle, tasks):
for value in tasks:
some_turtle.forward(value)
some_turtle.stamp()
some_turtle.right(30)
window = turtle.Screen()
bob = turtle.Turtle()
my_list = [10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120]
draw_thing(bob, my_list)

3.2. Turtle Coordinate List¶
Recall that you can use in to check for membership in a list as follows:
If a portion of your list is itself a list, you need to check for the entire sublist when using in.
If we wanted to keep track of a collection of coordinates (x and y pairs), we could do it by creating a list that contains sublists of coordinates. In the list below, three ordered pairs of coordinates are given:
coordinates = [[0, 0], [10, 20], [150, 80]]
x: 0, y: 0
x: 10, y: 20
x: 150, y: 80
To check if a specific x and y pair is in our coordinate list, we can use in as follows:
Note
Change the numbers in the if statement above to an ordered pair that is in the list, then run the code again.
Imagine that you wanted to create a simulation of a turtle walking around a grid world (in other words, the turtle would always turn by 90 degrees). Before each “step” the turtle takes, we will randomly choose to either turn left and move, turn right and move, or move straight ahead. Although we could move any amount for each “step”, let’s use a step size of 10. The following program implements this world, but is in an infinite loop. The program should automatically time out after running for 20 seconds in the browser (though if you are executing it in Thonny, you will need to press the Stop button).
Instead of having this program run forever, we would like the turtle to automatically stop the program whenever it walks onto a location that it has been before. In order to do that, we need to keep a list of coordinates that the turtle has been. Since the turtle begins at the origin, we will add [0, 0] to the list before any movement occurs. Since the turtle module keeps track of the turtle location using floating point values, the program will not behave the way you want if you simply store the current x and y positions in the coordinate list. Instead, we will convert the x and y values to be the nearest integer value, and store those in the list.
After every step that the turtle takes, we need to get the current x and y coordinates, in the form of [x, y]. If this ordered pair appears in the coordinate list, it means that we have been here before and we should end the program. If not, we need to add this ordered pair to the coordinate list and continue moving. The program below implements this behaviour.
3.3. The Return of L-Systems¶
Let’s return to the L-systems we introduced previously and introduce a very interesting new feature that requires the use of lists.
Suppose our L-System has the following rules:
X → F[-X]+X
F → FF
This L-system looks very similar to the old L-system, except that we’ve added the characters [ and ]. The meaning of these
characters adds a very interesting new dimension to our L-Systems. The [
character indicates that we want to save the state of our turtle,
namely its position and its heading (direction the turtle is facing) so that we can come back to this position later. The ] tells the turtle to warp to the most recently saved position.
The way that we will accomplish this is to use lists. We can save the
heading and position of the turtle as a list of 3 elements, like this: [heading, x,
y]. The index position 0 in the list holds the heading,
index position 1 in the list holds the x coordinate,
and index position 2 holds the y coordinate.
Now, if we create an empty list and every time we see a [ we append a
list that contains [heading, x, y], we create a history of saved places
the turtle has been where the most recently saved location will always be at
the end of the list. When we find a ] in the string we use the pop
function to remove the the most recently appended information.
Let’s modify our draw_l_system function to begin to implement this new
behavior.
When we run this example we can see that the picture is not very interesting, but notice what gets printed out, and how the saved information about the turtle gets added and removed from the end of the list. In the next example we’ll make use of the information from the list to save and restore the turtle’s position and heading when needed. We’ll use a longer example here so you get an idea of what the kind of drawing the L-System can really make.
3.4. Putting It All Together¶
To determine the instruction_string we used in the last example, we used an axiom of X and applied the following rules 6 times:
X → F[-X]+X
F → FF
If you run the code below, you will not see much happen. To fix the code below, you need to:
fix the
apply_rulesfunction so that the rules given above are appliedfix the call to
create_l_systemto use the correct axiom and number_of_iterations
Note
Once you have the code working, try it out with a larger number of iterations. You may also want to try this example with different values for the angle and distance parameters.
3.5. Practice Problems¶
3.5.1. Garden Herb¶
Here are the rules for an L-system that creates something that resembles a common garden herb. Use an angle of 27.5 degrees, and a distance of 5.
Axiom: H
Rule 1: H → HFX[+H][-H]
Rule 2: X → X[-FFF][+FFF]FX
If you iterated through the rules 5 times to create your instruction_string, and used a distance of 5, your code should have created something that looks like the following:
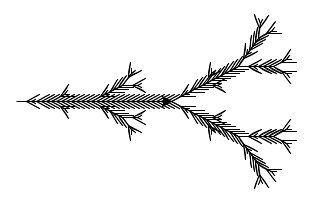
3.5.2. Branch¶
Here are the rules for an L-system that creates something that resembles a branch. Use an angle of 25 degrees, and a distance of 5.
Axiom: F
Rule 1: F → F[-F]F[+F]F
If you iterated through the rules 4 times to create your instruction_string, and used a distance of 5, your code should have created something that looks like the following:
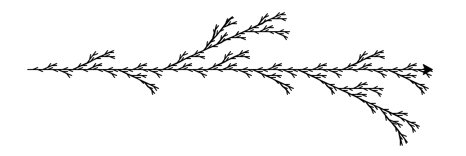
3.5.3. Symmetrical Branch¶
Here are the rules for an L-system that creates something that resembles a symmetrical branch. Use an angle of 25.7 degrees, and a distance of 5.
Axiom: X
Rule 1: X → F[+X][-X]FX
Rule 2: F → FF
If you iterated through the rules 5 times to create your instruction_string, and used a distance of 5, your code should have created something that looks like the following:
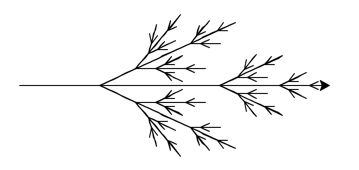
3.5.4. Seaweed¶
Here are the rules for an L-system that creates something that resembles seaweed. Use an angle of 22.5 degrees, and a distance of 10.
Axiom: F
Rule 1: F → FF-[-F+F+F]+[+F-F-F]
If you iterated through the rules 4 times to create your instruction_string, and used a distance of 10, your code should have created something that looks like the following:

3.5.5. Create Your Own¶
Experiment by creating your own rules for an L-system. Be sure to use the [ and ] characters in the rule(s) of your L-system.