11. Logical Operators¶
Quick Overview of Day
Introduce the logical operators and, or, not. Work on practice problems, in which students create programs that utilize logical operators. Booleans practice quiz.
CS20-CP1 Apply various problem-solving strategies to solve programming problems throughout Computer Science 20.
CS20-FP1 Utilize different data types, including integer, floating point, Boolean and string, to solve programming problems.
CS20-FP2 Investigate how control structures affect program flow.
CS20-FP3 Construct and utilize functions to create reusable pieces of code.
11.1. and, or, not¶
There are three logical operators: and, or, and not. The
semantics (meaning) of these operators is similar to their meaning in English.
For example, x > 0 and x < 10 is true only if x is greater than 0 and
at the same time, x is less than 10. How would you describe this in words? You would say that x is between 0 and 10, not including the endpoints.
n % 2 == 0 or n % 3 == 0 is true if either of the conditions is true,
that is, if the number is divisible by 2 or divisible by 3. In this case, one, or the other, or both of the parts has to be true for the result to be true.
Finally, the not operator negates a boolean expression, so not x > y
is true if x > y is false, that is, if x is less than or equal to
y.
Caution
Common Mistake!
There is a very common mistake that occurs when programmers try to write boolean expressions. For example, what if we have a variable number and we want to check to see if its value is 5,6, or 7. In words we might say: “number equal to 5 or 6 or 7”. However, if we translate this into Python, number == 5 or 6 or 7, it will not be correct. The or operator must join the results of three equality checks. The correct way to write this is number == 5 or number == 6 or number == 7. This may seem like a lot of typing but it is absolutely necessary. You cannot take a shortcut.
11.1.1. Check Your Understanding¶
- x > 0 and < 5
- Each comparison must be between exactly two values. In this case the right-hand expression < 5 lacks a value on its left.
- x > 0 or x < 5
- Although this is legal Python syntax, the expression is incorrect. It will evaluate to true for all numbers that are either greater than 0 or less than 5. Because all numbers are either greater than 0 or less than 5, this expression will always be True.
- x > 0 and x < 5
- Yes, with an and keyword both expressions must be true so the number must be greater than 0 an less than 5 for this expression to be true. Although most other programming languages do not allow this mathematical syntax, in Python, you could also write 0 < x < 5.
logical-operators2: What is a correct Python expression for checking to see if a number stored in a variable x is between 0 and 5?
11.2. Precedence of Operators¶
We have now added a number of additional operators to those we have learned. It is important to understand how these operators relate to the others with respect to operator precedence. Python will always evaluate the arithmetic operators first (** is highest, then multiplication/division, then addition/subtraction). Next comes the relational operators. Finally, the logical operators are done last. This means that the expression x*5 >= 10 and y-6 <= 20 will be evaluated so as to first perform the arithmetic and then check the relationships. The and will be done last. Although many programmers might place parenthesis around the two relational expressions, it is not necessary.
The following table summarizes the precedence discussed so far from highest to lowest.
Level |
Category |
Operators |
|---|---|---|
7(high) |
exponent |
** |
6 |
multiplication |
*, /, //, % |
5 |
addition |
+, - |
4 |
relational |
==, !=, <=, >=, >, < |
3 |
logical |
not |
2 |
logical |
and |
1(low) |
logical |
or |
11.2.1. Check Your Understanding¶
- ((5*3) > 10) and ((4+6) == 11)
- Yes, * and + have higher precedence, followed by > and ==, and then the keyword "and"
- (5*(3 > 10)) and (4 + (6 == 11))
- Arithmetic operators (*, +) have higher precedence than comparison operators (>, ==)
- ((((5*3) > 10) and 4)+6) == 11
- This grouping assumes Python simply evaluates from left to right, which is incorrect. It follows the precedence listed in the table in this section.
- ((5*3) > (10 and (4+6))) == 11
- This grouping assumes that "and" has a higher precedence than ==, which is not true.
logical-operators3: Which of the following properly expresses the precedence of operators (using parentheses) in the following expression: 5*3 > 10 and 4+6==11
Here is an animation for the above expression:
11.3. Practice Problems¶
11.3.1. Under 100¶
Write a program that takes in a number from the user, and correctly prints either “That number is between 1 to 100” or “That number is not between 1 to 100”. You may only use a single if/else block to solve this problem.
11.3.2. From Saskatchewan¶
Write a program that asks the user which province they live in. If the province isn’t “saskatchewan”, print out “You should come visit Saskatchewan sometime!”. You must use at least one logical operator in your solution.
11.3.3. Divisible by 3 or 5¶
Write a program that asks the user to enter a number. You should print out a message to the user, either “That number is divisible by either 3 or 5”, or “That number is not divisible by either 3 or 5”. Be sure to consider the data type of the input you are taking in from the user. Use a single if/else block to solve this problem.
11.3.4. Turtle Stuck In a Square¶
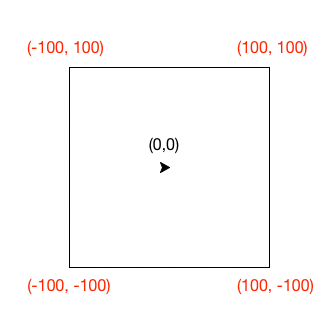
You have been given some starter code for the problem below. You only need to change one line of the code, specifically the line containing the while loop. Replace the word something with the appropriate boolean questions that will cause the turtle to continue moving until it gets to one of the edges of the square. Each time the program is run, the turtle will pick a new random direction to move. When executed, your program should look something like this:
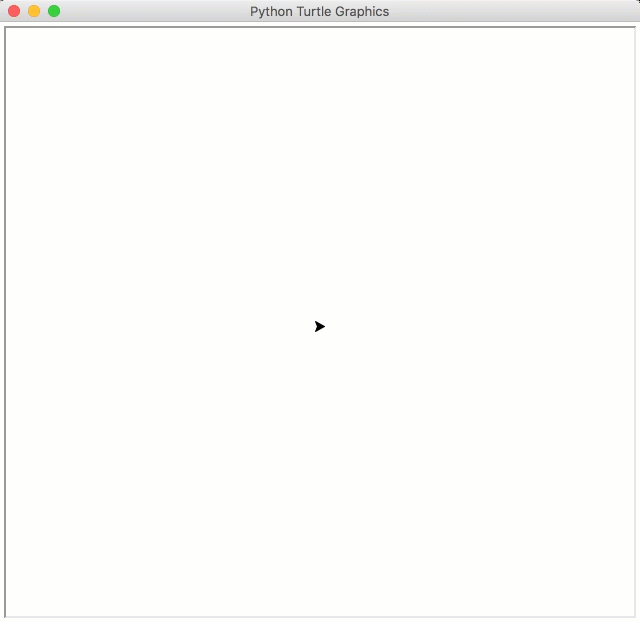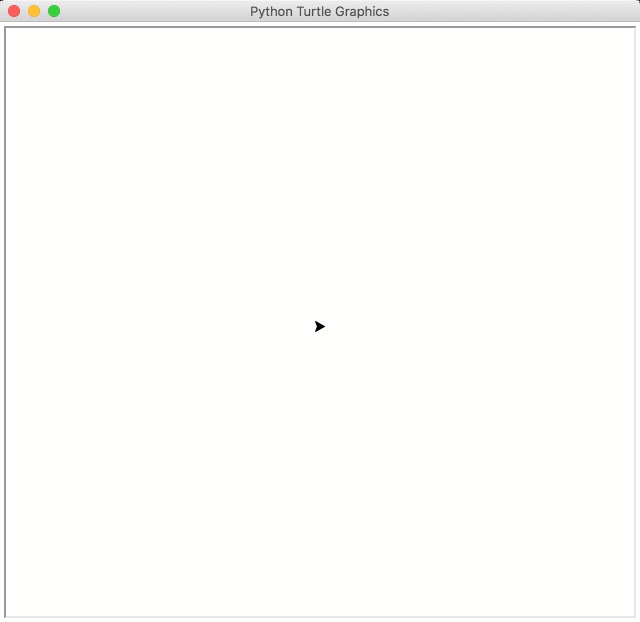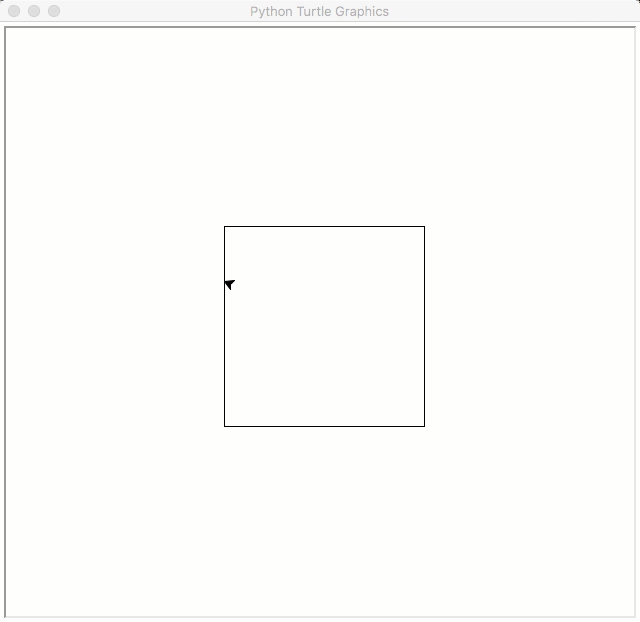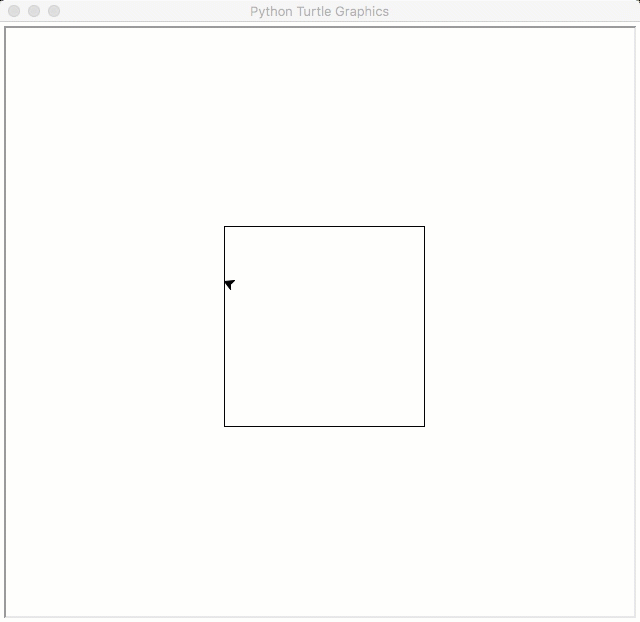
Note that you can get the current x coordinate of the turtle by calling bob.xcor(), and the current y coordinate by calling bob.ycor(). Also remember that the turtle begins at the origin (0, 0), which is in the center of the screen. The vertices of the square have x and y coordinates as shown below:
11.4. Booleans Practice Quiz¶
To confirm that you understand the boolean variables, you should try the Booleans Practice Quiz using only your brain (in other words, try to figure out what will happen without running the code).